TLDR

Exploration – trying new things, even when there are safe, familiar things within reach – is hard. Risky. Stressful. It’s also essential to a rich and vibrant life well lived. Like most other hard, stressful, important things, it’s better done together than apart. With our unique mixtures of shared and unshared experiences, we can use our gifts to help each other explore the world.

I

Let’s say you recently finished reading a novel, and are looking for a new book. You have many thousands of choices: classic fiction, science fiction, poetry, true crime, history, popular science, self-help, wisdom literature, politics…the list goes on and on. Authors you know, authors your friends read, authors you’ve never heard of that popped up while idly browsing Amazon. An impossible profusion of words, which you could dive through forever without seeing the bottom.

But you have to pick something, so let’s artificially constrain your options. Your long-time favourite novelist has a new book out, which you’re very excited about reading; you expect it to be much, much better than any random book you pick. At the same time, your friends have been raving about some obscure author you’ve never heard of, who wrote a lot of books in the 1960s, and you’ve been thinking of trying her out. Or you could try some poetry – you’ve never really gotten on with poetry, but you’ve also never read it much since you left high school. Maybe you’ll like it more now you’re a little older.

Which should you pick?

The simple approach is to pick the book that you expect to most enjoy. That’s clearly the one from your favourite novelist: you’ve yet to read a book from him that you’d give less than 8/10, and you’re confident this one will be another humdinger. Why gamble your precious time away on something new when you have a guaranteed win waiting on your bookshelf? Under this approach, you stick with what you know is good, unless you get a very strong recommendation from someone you trust.

Yet, this approach is clearly missing something. Most of us have had the experience of opening a book and discovering a whole new world inside: a kind of writing and a flavour of ideas you didn’t really imagine could exist until you experienced them. There was a time when you didn’t know your favourite author existed, yet now you’ve discovered him you can hardly imagine life without his books. Who knows how many other such authors are waiting out there for you to find?

What the stick-with-your-favourites approach is missing is all the other books you have ahead of you – a whole lifetime of reading, which could go very differently depending on what you discover in the meantime. Even if you expect to like the other books on your list less than your favourite author, you might be wrong – and if you are wrong, you can then read all of their other books too! The potential upside of a new discovery is huge, while the cost of being proven right is very limited – one disappointing book, or even less if you abandon it partway through.

What holds for authors holds even more strongly for genres. If you discover that you enjoy good history writing after all – or epic verse, or true crime – that unlocks a vast trove of books that had previously passed you by.

This asymmetry means that, paradoxically, the best decision can be to try an author or type of book you expect to be worse than your current favourite, if it has some realistic change of being better. How big the chance has to be before you take that bet varies based on circumstance, but the basic lesson is clear: when the cost of failure is one dull read, but the benefits of success can be reaped for the rest of your life, take risks.

Perhaps you should try that poetry collection after all.

II

Now imagine it’s Christmas time, and you’re looking for a gift for a friend. Let’s assume your primary goal is to benefit your friend – to make her happy, to enrich her life – not just signal that you care or fulfil a social obligation.

Again, there are countless options – but this time, your task is much harder, because you almost certainly know your friend far less well than you know yourself. As a result, for any given class of things you know she likes (wine, say, or cinema) you’ll very likely do a worse job of getting her something good than she would herself: some value will be lost in the gap between your mind and hers. The safe option is to get her something you both like, where you both trust your taste and are confident in her appreciation. Perhaps a really nice bottle of red, or a great board game you know she wants, or (in years other than 2020) a standing offer to take her out for dinner at a restaurant you both like. You’re almost certainly locking in some deadweight loss that way, but if you know your friend well it will hopefully be small, and perhaps made up for by the pleasure of companionship or the satisfaction of feeling valued.

Is there some way you can buy your friend a gift that is more valuable to her than what she would spend the money on herself? On the timescale of a single gift, that’s a tall order – you’re never going to know her preferences as well as she does. But on the timescale of a life? That might be a different story.

The principle is the same as before: the best choice on the scale of a single decision is often not the best choice on the scale of all future decisions, because choices that are risky now might open up whole new vistas of better choices in the future. What goes for choosing for yourself also goes for choosing for others. Except now you have a crucial advantage: a lifetime of unshared choices, of things-in-the-world that you have sampled and considered and judged about which your friend knows little or nothing.

You can use that unshared experience to help your friend explore, to pick out promising pieces of the Universe for her attention that she would otherwise have rejected on sight, or not considered at all. By distilling your experience, you can pick a gift with the potential to widen your friend’s horizons, to unlock years of potential choices she could not otherwise have made.

Let’s make this concrete. Suppose you and your friend are both avid readers. There are some genres you both read a lot of – say, historical fiction – and there are genres you read that she does not – say, science fiction. You recently finished both a Booker-winning historical novel, and a Nebula-winning sci-fi novel, and loved them both. You’re pretty confident your friend hasn’t read (or bought) either. Which should you get her?

The Booker winner is the safe choice. You’re confident she’ll love it, it’s very much in her wheelhouse. But you’re also confident she’s heard of it, and will get around to reading it sooner or later without you. Maybe she’ll love reading it even more if it comes from you, and that’s not nothing. But this isn’t a gift that will expand her horizons.

The Nebula winner, though – that’s a different story. That’s a risky gift. There might well be a good reason she doesn’t read sci-fi – maybe she tried several of the classics as a teenager and hated them all. There’s a much higher chance that your gift falls completely flat than if you bought her the Booker winner, or a fancy bottle of gin. But if it doesn’t fall flat, if she tries it and loves it against her own expectations, you might just unlock a whole new world of art and literature that had previously passed her by.

If you’re thinking only about which gift will most benefit your friend in itself, you should probably get her the Booker. But if you’re thinking about what gift might most benefit your friend over a lifetime, you might want to get her the sci-fi.

III

Exploration is hard. Striking out into new territory is risky, stressful and often unrewarding – it’s so much easier to retread familiar ground. But without exploring, we are doomed to miss out on countless opportunities to live richer, happier lives.

Luckily, we are surrounded by people who have lived different lives from ours, who have explored parts of the world we have never seen. If we can access even a fraction more of that unshared experience, our own exploration becomes easier, more rewarding – and more fun. Like most difficult things, exploration is better done together than apart.

Treating gifts as an opportunity for free exploration has several benefits. Firstly, it can be an essential prompt to explore at all, when our habits and routines and the demands of everyday life act to pull us ever deeper into placid, unvarying orbits. Secondly, it makes that exploration easier, more effective, and more enjoyable: how much better to start your exploration of some new place with a thoughtful guide, than to dive sightless into an unknown sea? Finally, it might just help us make better gifts: gifts that are more alive, more interesting, that communicate more about ourselves and our hopes for each other.

Treating gifts as exploration can, admittedly, be dangerous: good exploration must be risky, and risky things often fail. A pile of gifts-as-exploration will contain many interesting things, but also many things that their recipients definitely do not want. Failed exploration, especially when imposed by others, often does not feel like a noble venture sadly thwarted, but like a slap in the face: how could you possibly think I would like…?

On the other hand, it’s not as though our existing gifting habits don’t frequently lead to abject failure: we’re all well-trained from childhood when it comes to graciously receiving gifts we dislike. This can actually frustrate attempts to treat gifts as exploration: you can’t get someone a better explore-gift next time if you don’t know how flat your last one fell. But it does mean that we give each other some degree of cover to take more risks.

Exploration might not always be the right theme in one’s gifts for others: that depends on the tenor of your relationship with your giftee, your mutual tolerance for risk, your pre-existing norms of giving and getting. But even if you don’t feel comfortable getting your friends and loved ones really out-there exploration gifts (“Here, grandma, try this Deadpool comic”), you can probably push the envelope a little, shift the locus of your giving a little more in that direction. You can raise the topic in advance, suggest moving your mutual giving in a more exploratory direction. See what they say.

Above all, you can tell your friends and loved ones that what you would most like for Christmas this year is the chance to share some part of their life that you haven’t seen before.

Crossposted from LessWrong.

TLDR

• Final Version Perfected (FVP) is a highly effective algorithm for deciding which tasks from your To-Do lists to do in what order.
• The design of the algorithm makes it far more efficient than exhaustive ranking, while (in my experience) far more effective than just reading through the tasks and picking one out.
• FVP is most useful when you have a large number of tasks to choose from, don’t have time to do all of them, and are initially unsure about which is best.
• I find FVP very effective at overcoming psychological issues like indecision, procrastination, or psychological aversion to particular tasks.
• Currently there are limited online tools available, and I mostly use FVP with paper lists. Ideas (or tools) for better online execution of FVP would be very valuable to me.

Introduction

Execution is the Last Mile Problem of productivity infrastructure. You can put as much effort as you like into organising your goals, organising your To-Do lists, organising your calendar, but sooner or later you will be presented with more than one thing you could reasonably be doing with your time. When that happens, you will need some sort of method for choosing what that thing will be, and actually getting started.

Most people, I think, face this problem by either just doing the thing that is top-of-mind or looking through their To-Do list and picking something out. This works fine when the next thing to do is obvious, and you have no problems getting started on it. But when you have many potential things to do and aren’t sure which is best, or when you kind of know what the best next thing is but are avoiding it for one reason or another, you need a better system.

That system needs to be quick to execute, easy to remember, and effective at actually having you do the best next task. It needs to be robust to your psychological weaknesses, minimising procrastination, indecision, and ugh fields. It needs to be efficient, requiring as little work as possible to identify the most valuable task.

Enter Final Version Perfected.

The FVP Algorithm

The algorithm for executing tasks under FVP is pretty simple. You can find a description of it by the designer here, but here’s my version:

1. Put all the tasks you have to choose from into one big unsorted list.
2. Mark the first item on the list. Don’t do it yet.
3. For each subsequent item on the list, ask yourself, “Do I want to do this task more than the last task I marked?” If yes, mark it. If no, don’t mark it. Move on to the next item.
4. When you reach the end of the list, trace back up to find the bottom-most marked task. Do it, then cross it off the list.
5. Beginning with the next unmarked task after the task you just crossed off, repeat step 3, comparing each task to the bottom-most uncrossed marked task (i.e. the one prior to the one you just crossed out).
6. Go to step 4. Repeat until you run out of time or list items.

In FVP, then, you perform a series of pairwise comparisons between tasks, in each case asking whether the new task is something you want to do more than the old task. The “want to do more than” comparison is deliberately vague: Depending on context, it might be the thing that would best move your project forward, the thing that would have the worst consequences if you didn’t do it, or the thing you would most enjoy doing. The key thing is that at each stage, you’re only comparing each task to the most recent task you marked, ignoring all previous tasks.

I’ll talk more in a moment about why I think this algorithm is a good one, but first, let’s work through an example. (If you’re sure you already understand the algorithm, click here to go straight to the pros and cons.)

A long-ish example

Let’s say this is my to-do list for today:

• Buy milk
• Finish term paper
• Play video games
• Work out
• Save the world
• Walk the dog

I start by marking the first item:

• × Buy milk
• Finish term paper
• Play video games
• Work out
• Save the world
• Walk the dog

Then I compare it to the next item on the list. Which do I want to do more, finish the term paper or buy milk? Well, the term paper is due today, and I don’t need milk until tomorrow, so I decide to do the term paper first.

• × Buy milk
• × Finish term paper
• Play video games
• Work out
• Save the world
• Walk the dog

Moving on to item 3. I already decided I want to finish the term paper before buying milk, so I can ignore the milk for now. Do I want to play video games or finish my term paper? Well, in some sense I want to play video games more, but my all-things-considered endorsement is to finish the term paper first, so I leave item 3 unmarked.

Next, item 4: do I want to finish the term paper or work out? Well, in some sense I’d rather not do either, and in another sense the term paper is more urgent, but working out is important, I’ve heard it has cognitive benefits, and I know from experience that if I don’t do it first thing I won’t do it, so it takes precedence:

• × Buy milk
• × Finish term paper
• Play video games
• × Work out
• Save the world
• Walk the dog

Item 5: oh yeah, I forgot, I need to save the world today. Damn. Well, I can’t work out if there’s no world to work out in, so I guess I’ll do that first.

• × Buy milk
• × Finish term paper
• Play video games
• × Work out
• × Save the world
• Walk the dog

Ditto for walking the dog: much though I love him, I won’t have anywhere to walk him if I don’t save the world first, so that takes precedence again.

I’ve finished the list now, so it’s time to do the last item on the list. Looks like that’s saving the world. Luckily, it doesn’t take long:

• × Buy milk
• × Finish term paper
• Play video games
• × Work out
• × Save the world ✓
• Walk the dog

Now that I’ve done the highest priority task on the list, I go back to FVP to determine the next one. There’s actually only one comparison I need to make: work out or walk the dog? Walking the dog can wait until the evening, so it’s time to head to the gym.

• × Buy milk
• × Finish term paper
• Play video games
• × Work out ✓
• × Save the world ✓
• Walk the dog

Again, there’s only one more comparison I need to do to determine my next top task: do I want to finish my term paper, or walk the dog? And again, walking the dog isn’t that urgent, so I spend a few hours on the term paper.

• × Buy milk
• × Finish term paper ✓
• Play video games
• × Work out ✓
• × Save the world ✓
• Walk the dog

Now I’m all the way back to the top of the list! But now there are two more comparisons to make to decide on the next task. First, do I want to buy milk, or play video games? I’ve worked pretty hard so far today, and buying milk isn’t that important, so let’s play games first:

• × Buy milk
• × Finish term paper ✓
• × Play video games
• × Work out ✓
• × Save the world ✓
• Walk the dog

Finally, do I want to walk the dog or play video games? The dog has been waiting for hours for a walk now, and I could do with some fresh air, and I’d feel guilty just gaming without taking him out, so let’s do that first:

• × Buy milk
• × Finish term paper ✓
• × Play video games
• × Work out ✓
• × Save the world ✓
• × Walk the dog

There’s no unmarked tasks in the list now, so to finish I just work up the list in order: first walking the dog, then playing games, then, finally, buying milk.

FVP: Why and why not

The usefulness of FVP depends on a few key assumptions.

• Firstly, the algorithm assumes your preferences are transitive, and that you can accurately assess the value of each task according to your preferences. These are pretty fundamental assumptions that will be integral to almost any list-based execution system. In reality, your preferences probably aren’t quite transitive, but hopefully they are close enough that pretending they are is reasonable. As for accurately assessing each task, well, no execution algorithm can prevent you from making any mistakes, but FVP is more effective than most at eliciting your best guesses.
• Secondly, FVP assumes that your preferences are stable over the timeframe you’re using it. If your preferences shift substantially over that period, such that you need to re-prioritise among the existing tasks on your list, you’ll need to throw out your previous FVP and start again. This places some constraints on the timescale you can organise using a single FVP iteration: I seldom stick with the same iteration for longer than a day. (Note, though, that FVP can handle the addition of new tasks quite easily, as long as they don’t alter the existing order.)
• Thirdly, the value of FVP is greatest when you are unsure about which task you should do next, and especially when you don’t have time to do every task you might want to do that day. I find FVP most useful when I have a lot of different tasks competing for my time; it is much less useful when my time is pre-allocated to a single, well-planned-out task.

When these conditions are met, FVP is a very effective method for guiding action. It is both efficient and exhaustive: guaranteed to identify the top-priority task while avoiding most of the work involved in producing a complete ranking. It is a simple algorithm, easy to remember and quick to perform. After doing it for a while, I find it scarcely requires conscious thought – but still reliably identifies the most valuable task for me to work on.

The biggest benefit I get from FVP, though, is how much easier it makes it to do important things I’d rather avoid. There is something about a bald, pairwise comparison between two tasks that is highly effective at overcoming my aversion to difficult things. If an important but unpleasant task is nestled within a long to-do list of minor-but-rewarding busywork, it is easy for my eye to skip over the difficult task, defer it till tomorrow, and work on something more pleasant instead. It’s much harder to do that when comparing the important task to each minor task in isolation.

FVP is also good at minimising time lost due to indecision. When presented with a menu of tasks to choose from, it can be quite hard to select a single task to work on first. When that choice process is reduced to a series of simple pairwise comparisons, the choosing process as a whole becomes much easier. And, once I’ve finished with FVP and selected a single winning task, there’s an impetus towards starting that makes me much less prone to procrastination.

One last brief note on infrastructure: due to its relative obscurity, I haven’t found great online tools for FVP. Complice’s starred-task system can be passably adapted to the algorithm, but in general I’ve found physical paper lists to work best. When I was at work I would print off my Todoist task lists and use those; now I’m working from home I mostly write them out by hand. This is kind of time-consuming and redundant, so if you dislike paper notes and don’t have access to a printer it might be a significant mark against FVP.

I’d really love it if someone created a great online tool for FVP or integrated it more formally into an existing productivity application, but I don’t expect that to happen any time soon. In the meantime, if you have ideas for existing ways to execute FVP online, I’d love to hear about them!

Over the course of this all-too-solitary year, a few different people have asked me for video game recommendations. I generally responded with overwhelmingly long lists that probably did more to scare them away than anything else. But with a long, dark winter approaching and the pandemic still keeping most of us at home, it seems like a better time than ever to explore a few new corners of the digital world. So, here’s a shorter list, in no particular order, of ten not-too-long, more-than-minimally-obscure games I really, really think you should play.

Return of the Obra Dinn

Once upon a time, Lucas Pope made Papers Please, a very stressful game about guarding the border of a totalitarian state. Then he disappeared for five years. In 2018, he resurfaced with one of the best games I have ever played.

Once upon a time, the Obra Dinn set sail from England, bound for Formosa. Then it disappeared for five years. Now it has reappeared off the English coast, derelict, and the East India Company has sent you to find out what the funk happened.

Armed with a ship’s manifest, a map of the ship, pictures of the crew, and a magic watch that lets you relive the last few seconds of a corpse’s life (standard issue for insurance agents in the 19th century), you must identify the fate of each of the 60 crewmembers. Oh, and the whole thing is meticulously rendered in 1-bit graphics.

In essence, Return of the Obra Dinn is one huge puzzle – perhaps my favourite puzzle in any video game I’ve played. By paying attention to everything that’s going on in every scene, you slowly piece together who is who, and what happened to them. You never need to guess: every identity and every fate, however obscure, is specified by some telling detail somewhere. It’s enthralling, especially once the story starts to get moving and you find out more and more about what happened to this misbegotten ship and her unfortunate crew. It’s hard to say more without spoilers; let’s just say that dithered explosions are surprisingly beautiful.

I played Obra Dinn straight through in about seven hours, while bedridden with a nasty cold. My incapacitated state made me take more leaps of guesswork than I might otherwise have done, which I will regret forever: the characters etch themselves into your brain so deeply that the game is basically un-replayable, so I’ll never get the chance to discover those answers the right way. If you take me up on this recommendation, learn from my example, and approach this game with the patience it deserves. It’ll probably still take you less than 10 hours (though no shame if it’s longer!), and It’s well worth the effort.

The Stanley Parable

“When Stanley came to a set of two open doors, he entered the door on his left.”

The Stanley Parable is a very, very hard game to review. Firstly, because it is so strange, so unlike anything except itself. Secondly, because it’s so difficult to write about any aspect of it without diminishing the experience of discovering it for yourself.

Which is not to say I don’t have thoughts about it! I wrote a whole thing here about all the different possible interpretations of The Stanley Parable and how they all, one by one, fall by the wayside, until all that is left is the thing itself, glorious and hilarious and free. But eventually I decided even that was too spoilery, and cut it in favour of this…thing.

Look, it’s really good, okay? It’s funny and smart and meta in all the best ways. It handles the question of choice in video games, which really is the only new thing videos bring to the table in terms of Art, with more wit and intelligence than any other game I’ve played. It’s not a long game, unless for some weird reason you end up playing it over and over and over and over and over again, but who would do something like that?

Luckily the free demo does a pretty good job of telling you whether or not you’ll enjoy the game, while…agh, just play the demo, it’s good – though not quite as good as the real thing.

There is, it is rumoured, an expanded version in the works, but since that version (a) is likely to be substantially different, and (b) has been delayed several times, you’re probably better off just taking the plunge now. If you’re anything like me, you’re unlikely to regret the opportunity to play it again in a year or two.

Shadowrun: Dragonfall and Shadowrun: Hong Kong

As a setting, Shadowrun confuses me. It really shouldn’t work. At first glance it’s the worst kind of incoherent coolism, the kind of setting whose operative principle is “Sure, why not?”. Want to play an elf that can do awesome magic and is also a wicked cool cyberpunk hacker? Want to control an army of mechanical drones, and an army of spooky elemental spirits? Sure, why not? Want to fight against a nefarious megacorporation who are also powering their evil machines with the souls of the dead? Sure, why not? Throw in the kitchen sink while you’re at it, might as well.

Yet, it works. In some ways it works much better than other fantasy settings, because it doesn’t assume that worlds different from ours must be technologically static. Magic re-emerged into the world, things changed and people died, and the world kept on going. Now it’s decades later, and the dragons have realised that you can get richer on the stock market than you can hoarding treasure, and the corporations have learned which problems are best solved with technology and which are best outsourced to the shamans.

Harebrained Schemes’ first entry into the Shadowrun universe, Shadowrun Returns, was, in my opinion, not very good. But the two games it followed up with, Shadowrun: Dragonfall and Shadowrun: Hong Kong, are two of my favourite RPGs. Each is in a lovingly realised setting, with gorgeous backdrops, lots of interesting missions, and – especially in Hong Kong – characters I actually cared about. Crucially, neither outstays its welcome, with both being much shorter than your average (gargantuan) cRPG.

In gameplay and overall style, the two games are essentially the same, though Hong Kong is a little slicker. At the heart of both games is the classic Shadowrun concept: corporate espionage, exfiltration, the occasional assassination job if you have the stomach for it. It’s a nasty business, essentially organised crime, and most of the people who do it are nasty folks, but somehow the games always find a way for you to be a hero, if you want to be (in Dragonfall I was; in Hong Kong I wasn’t).

(It’s probably worth noting here that these are by far the most combat heavy of the games on this list (though not the most explicitly violent – that would be Obra Dinn), so if you’re not interest in having your cyberpunk worldbuilding interspersed with mowing down armies of mech-armoured, spellslinging goons then these probably aren’t the games for you.)

More important than the missions, though, is the world they inhabit, and it’s here that both games shine. Both achieve what many RPGs fail to, and make 2050s Berlin and Hong Kong (respectively) feel like living, breathing places – I can’t comment on the plausibility of the Hong Kong setting, but I found 2050s cyberpunk Berlin surprisingly believable, all things considered. Neither the cyberpunk nor the fantasy tropes are especially original by themselves, but in the interweaving of the two both games find that special something that makes the Shadowrun setting shine. Both also have surprisingly deep dialogue trees and character development for many minor NPCs; in Hong Kong in particular, I got quite invested in all the little lives going on around me in our little shanty-town home base.

In terms of setting and storyline, Hong Kong is probably the better game; in terms of combat I think Dragonfall offers a more interesting challenge, though that might just be because I built my character better in Hong Kong. Both are well worth your time and money.

To The Moon

I don’t honestly remember whether or not I cried at the ending of To The Moon. I do remember feeling more emotionally conflicted about it than basically any other game I’ve played.

I got the game in some Humble Bundle years ago. Tried it, bounced off the graphics and the gameplay style, and forgot about it for years. At some point a friend mentioned that it was one of her favourite games, and I was interested enough to try it again. Turns out, abandoning it the first time was a huge mistake.

The setting: Sigmund Corp is a company that sells deathbed wishes. You want to be president, or marry the love or your life, or become a billionaire? Sigmund can give it to you. Just sign the contract, hand over the fee, and when you’re dying they’ll come and edit your memories, ensuring you die happy in the knowledge of a life well-lived.

Is that a…good thing to do? Hard to say. It’s a great thought experiment, though, and it’s excellently – and traumatically – handled here.

In To The Moon you play as a team of Sigmund scientists, dispatched to fulfill its contract with Johnny, an old man slowly dying in a big house. Johnny wants to go to the moon – simple enough, the kind of wish you handle all the time. The problem, as you quickly discover, is that he doesn’t remember why. So begins a traversal back though a lifetime of memories, trying to discover work out what to change to give Johnny whatever it is that he really wants.

Telling a story backwards is not a new trope, but it’s one that’s difficult to pull off well, and To The Moon does so with flying colours. It’s a story with no shortage of Themes, which it (mostly) handles with depth and grace, if not always with subtlety. The music is stunning, some of the best I’ve ever experienced anywhere, a fact made even more remarkable by the fact that it was all composed by the game’s lone developer.

There are wrinkles. I still don’t get on well with the graphics style, or the game engine. The humour is a mixed bag, sometimes charming and sometimes irritating. The game can’t quite bring itself to be a pure walking simulator, and insists on wedging in silly minigames that add nothing to the overall experience. But I’m willing to let all of these annoyances slide, because the thing in its entirety is so beautiful.

Dear Esther

Of all the games on this list, I expect Dear Esther to be the most YMMV. A game in which you slowly walk around a windswept island, with no run or jump buttons, no goal except to keep going, hear what the game wants you to here and see what it wants you to see…is not going to be for everyone. But at a pretty important time in my life, it was for me.

Of all the various emotions you might encounter over the course of a life, the one games are least well-equipped to reckon with is sadness. Excitement, joy, curiosity, wonder, fear, anger, disgust: all are well-represented in the gaming canon. But sadness, depression, grief are slow, heavy, aimless things, ill-suited to the high-intensity engagement of most popular games. Any game that would seriously reckon with these slow, tired, lonely feelings must itself feel slow and tired and lonely: hardly a recipe for a money-spinner.

Nevertheless there is a small but persistent line of games attempting to deal with these kinds of experiences. Of these, Dear Esther is the one that found me when I needed it.

You play as a man on a desolate island, alternately scenic and oppressive. You’re not initially sure why he’s here or what he’s talking about in his erudite-yet-roundabout narration, but it becomes clear he’s circling around some deep wound he doesn’t quite dare to touch. The music is beautiful, some of my favourite in gaming, expertly calibrated to the mood of the place. The first part of the game is admittedly a very slow start; but as you go on, and the narrator starts to lose his composure, and night begins to fall, the game becomes both more vivid and more intense. From about the halfway point on, I would call all of it – not just the audio – beautiful.

The game also rewards replaying: because it’s so short, because the narrator’s audio is somewhat randomised so you never hear exactly the same thing each time, and because the things you learn later cast substantial parts of the earlier game into a different light.

The rest is spoilers. Your mileage may vary. Perhaps it won’t speak to you. But it’s one of my favourite games, and it’s short enough and cheap enough that I think it’s worth trying.

Spider and Web

I couldn’t quite resist putting a text adventure on this list. There are actually quite a few text adventures I like a lot, but they are admittedly pretty niche, so I’m restricting myself to one full entry, and a few links. Andrew Plotkin’s Spider and Web made the cut because it tries to do something I’ve never quite seen in any other game, and does so well.

In general, we should expect text adventures to be at their best when they try to do things that are difficult to do effectively with graphics but can be done very effectively with words. Surreal humour is one example; creepy cosmic horror is another. Spider and Web is an example of a third thing: editing the narrative. Unreliable narrators are an underused trope in video games, one for which I’d generally expect text adventures to have a somewhat better time than graphical games. In Spider and Web, the unreliable narrator is you.

You begin in an unremarkable alleyway in an unspecified city, facing an unmarked door. Why are you here? You certainly don’t have anything suspicious in your pockets that could open such a door; in fact your inventory is empty. Oh, well. You turn and leave.

Bright lights. An interrogation room. Your interrogator is not impressed. Obviously you didn’t just turn and leave, because they found you behind the door. Try again.

On it goes. You get past the door. You infiltrate the facility. You turn left and burst into the laboratory complex! No, you would have been spotted immediately, and you weren’t caught until later. You must have gone a different way. Try again.

It’s a hard game, sometimes viciously so. You need to simultaneously solve the immediate puzzles of espionage, while also keeping an eye out for little ways to get the jump on your interrogators. Most of the time, they catch you at it; occasionally, they don’t. If you fail enough times the interrogator starts making little comments about how he’d expect a spy of your calibre to be a little smarter. The puzzle at the turning-point of the game is fiendishly hard – I’m pretty sure I used a walkthrough, or at least got some hints. But it’s also so clever I found it hard to fault it for being so difficult.

Like most text adventures, Spider and Web has the significant advantage of being free, at least if you discount the time required to get used to the basic conventions of the genre. You can run it on your command line if you’re feeling hacker-y, but dedicated software like Lectrote (by the same author as the game)can make the experience a little more friendly. If you like it, good news! There’s a whole little world of free interactive fiction waiting for you, much of it rather good.

Disco Elysium

Okay, back to the world of pictures.

Of all the games on this list, Disco Elysium is the only one I discovered this year. I picked it up at the height of the first COVID wave, in the midst of my worst depression relapse for years, on the advice of a rather odd review in Rock Paper Shotgun. I needed to stop thinking for a couple of days and play something interesting. Usually when I decide to buy a new game it takes me several tries to find one that hooks me; this time, somehow, I got it in one.

It’s actually quite easy to describe Disco Elysium in a few words: it’s a dialogue-centric black-comedy not-quite-sci-fi police-procedural RPG.

Okay, that was quite a few words, especially if you don’t count the hyphens. The fact is, while many individual aspects of Disco Elysium can be seen as quite traditional, their combination is very original indeed.

Firstly, it’s funny. Much funnier than any other RPG I’ve played. I laughed out loud quite a few times, and spent much of the rest of my playthrough smirking. Most of that humour comes from the shenanigans of your player character’s deeply messed up inner psyche: in Disco Elysium, your skill points represent both abilities and facets of yourself, and the more points you put in one facet, the more liable that facet is to butt in at inopportune moments.

Put points into Authority and you become more imposing, but also more boorishly status-obsessed. Put points into Inner Empire and you get more imaginative, but more prone to tear off on wild flights of fancy. The different aspects have their own voices, sometimes even their own voice actors, and their frequent internal disagreements are very entertaining.

The rest of the humour comes from the game’s huge cast of NPCs, many of whom are delightfully catty. Because that’s the second thing about Disco Elysium: it’s political. And not in the regular right-great-wrongs kind of game politics, but the grubby, down-to-earth, endlessly-argued-about, real-world kind of politics. You can even pick your own politics…to some degree. I went for a combination of moderate and libertarian, but rather than manifesting as a kind of moderate capitalist, my character lurched wildly between mealy-mouthed do-nothingism and unabashed greed-is-good Randianism, to the great confusion of my long-suffering sidekick.

I’m actually not sure where the game makers’ own political sympathies lie, which is its own kind of triumph: I think they’re probably self-aware leftists, but I wouldn’t bet much money on it. The leftist characters in the game certainly aren’t treated any more kindly than the rest; if anything, the reverse is true. The only group the game seems to have nothing but contempt for (other than the racists) are those who try to avoid politics altogether by agreeing that everyone makes some good points.

Anyway. The plot of Disco Elysium takes the form of a police procedural, investigating a politically charged murder in a gruesomely poor part of a rundown city. Oh, and to keep things interesting your main character has the kind of retrograde amnesia you only ever get in fiction, and needs to work out who the hell he is along with everything else. The setting of Disco Elysium is…odd. Unsettling. In many respects, it is a world far more like our own than the settings of most RPGs, while in other respects it is a very alien place. I don’t think I would like to live there, but I cared about the people who do.

The gameplay of Disco Elysium takes the form of an RPG of sorts, though one based entirely around dialogue and skill checks, with almost no combat in the traditional sense – no point where one set of rules gives way and another, more violent set of rules takes temporary hold of the world. Since the main turn-off of most RPGs for me is the way they scatter a perfectly good plot amidst dozens or hundreds of hours of goblin-slaying, this is fine by me.

All in all Disco Elysium is my favourite new game since…well, since Return of the Obra Dinn, to be honest, which is only about two years’ distance. But still, it’s a very good game and I strongly recommend it, especially to those of you who wouldn’t normally consider playing an RPG but are interested in trying something different. At the very least, it’s made ZA/UM one of the very short list of developers I’m actively keeping an eye on, waiting to see what they do next.

Primordia

In the world of modern-but-retro point-and-click adventure games – a world that’s been undergoing a modest revival over the past decade or so – Wadjet Eye Games is king. As a fan of such games I’ve played and liked most of their line-up, both as developer and as publisher, so picking a game to recommend here was a conundrum. Their best game is probably Technobabylon, a huge and sprawling cyberpunk mystery story with many characters and many – perhaps too many – creative mechanics. But Technobabylon isn’t my favourite Wadjet Eye game. That honour would have to go to Primordia.

I thought that was a controversial opinion. Back when I got Primordia (for cheap in a GOG sale, as I recall), it had received mostly lukewarm opinions from critics. Many said that the story didn’t hold together that well, or that the comedy sidekick was kind of annoying (both true). But I see now that it has 97% positive reviews on Steam, which is flabberghastingly high, so apparently it’s not as controversial an opinion as I thought.

Agh, I’m watching the trailer on Steam now and it’s giving me chills. I love its aesthetic. That melancholic, rusty intricacy gets me every time. The humans have gone, and left behind only lost little robots and haunting music.

Perhaps I should step back.

In Primordia, you play as Horatio Nullbuilt, a lonely robot in a crashed airship in a desolate, war-scarred landscape. You spend your day scavenging parts, keeping yourself alive and trying not to think too hard about the big robot city nearby, a city that saturates the airwaves with its propaganda, a city you hate without knowing why. But one day, when a robot from the city cuts its way into the ship and steals your power core, you have to choose between joining the rest of the landscape in slow, fatal decay, or reckoning with your hatred, and your history.

That’s how I’d’ve put it, anyway. Maybe that’s why they don’t pay me to write blurbs for video games.

There is so much about Primordia that doesn’t make sense. Almost all the robots are obviously just metal humans, totally unbelievably like us in every respect. The history of Metropol barely holds together. Many key plot points hang on slender threads of suspended disbelief. But I don’t care because I love it all. I love the music. I love the mellifluous voice of the antagonist and the husky robotic tones of our hero (voiced by the narrator from Bastion!). I love the decaying, rust-ridden world. I love the totally implausible culture the robots have built for themselves since the humans went (especially the surnames, let me tell you about the surnames…except don’t, because spoilers). I love the great old robots of the city, vast and slow like ents of steel and silicon and rust, and the ruthless political games they play.

I’m baffled that a game this short could pack so much into itself that it keeps unspooling in my memory, all these years later. Somehow, so much more of it has lodged in my memory than usual that my mind, used to reconstructing big experiences from tiny slivers of memory, assumes there must really have been far more of it than there was. But that in itself tells you how memorable it was, how well it is the thing that it is.

I hear the developers have a new game out soon, also published by Wadjet Eye. I’ll definitely be keeping an eye on that. In the meantime Primordia is so old and cheap now that, really, what excuse do you have not to play it?

Journey

As this blog post makes clear, there are many games I’m very happy to evangelise about. But there’s only one game I’ve ever more-or-less forced my friends and significant others to play. Last but not least, let’s talk about Journey.

Journey’s beauty is, I think, uncontroversial. It is also many-faceted. The style of its ruined art and architecture – some mashup of ancient Egypt, classical Islam, and Shadow of the Colossus – is big and solemn and imposing, a fitting match to the solemn grandeur of the desert, and of the everpresent mountain. The game’s use of light and shadow is masterful, conjuring powerful and repeating cycles of safety and danger, purity and corruption, good and evil. The music is great, especially the song that plays over the closing credits, soaringly marking your…ah, but that would be telling.

But what really makes the game shine, quite literally, is the sand. I’ve never seen sand like this before, in the real world or any other game. I never get tired of watching it: it glitters like a sea of gemstones, shifting colours vividly from level to level as the light changes. The game reaches its first apotheosis at sundown, when the sand shines like gold against the enormous setting Sun. Just its first apotheosis, mind – there are more to come.

In addition to its visual beauty, Journey is also a masterclass in nonverbal storytelling. There is not a single word of dialogue in the entire game: you piece together the story from abstract, wordless visions and long-abandoned murals. You need to go slowly and carefully – or play several times – to really understand what’s going on, but once you do it adds a layer of once-hidden meaning to everything you see. There is no other game I enjoy watching other people play as much as this.

Gameplay wise, Journey is simple: a little more mechanically complex and involved than a walking simulator, a little less than any other kind of game. Yet despite their simplicity the mechanics work wonderfully. Jumping and gliding are joyful; failing and falling hurt. I was particularly impressed by the game’s mechanics of gameplay and loss: you can’t die, so you’d think the game’s enemies would hold no fear, but in fact they can harm you far more enduringly and meaningfully than in a game with higher lethality and at-will saves.

Mind, that’s in the PS3 version. For all I know the PC version has at-will saving and so has given up that particular gem of design. But! As of 2020 there’s a PC version on Steam, which you should all immediately go and buy. I can’t physically sit you down in front of my TV and hand you a controller, but this is me doing it in spirit: buy Journey. Play it. Share it with your friends. Spread the good word.

Oh, and those other games I mentioned up above are pretty good too. Maybe check those out while you’re at it.

• The NSA has released an archive of old security posters. (h/t Schneier on Security).
• There is a unit of radiation called the banana equivalent dose (h/t The Prepared).
• “[I]f the chief executive officer of a public company commits sexual harassment, he is probably also guilty of insider trading“.
• “‘Like my cat, I often simply do what I want to do.’ This was the opening sentence of Derek Parfit’s philosophical masterpiece, Reasons and Persons… However, there was a problem. Derek did not, in fact, own a cat. Nor did he wish to become a cat owner, as he would rather spend his time taking photographs and doing philosophy. On the other hand, the sentence would clearly be better if it was true. To resolve this problem Derek drew up a legal agreement with his sister, who did own a cat, to the effect that he would take legal possession of the cat while she would continue living with it.”
• China’s Supreme People’s Court is not happy with Wuhan police for suppressing “rumours” of a pneumonia outbreak: “It … undermines the credibility and chips away at public support for the Communist Party. It could even be used by hostile overseas forces as an excuse to criticise us.”
• Speaking of hostile overseas forces using this as an excuse to criticise China, Scott Sumner argues that authoritarian nationalism is bad for your health.
• The robots are coming for your blood.
• Grey seals clap underwater to show dominance (maybe).
• Speaking of seals, did you know some fur seals in Antarctica have sex with penguins? Sometimes they eat the penguins afterwards, sometimes they don’t.
• “Gun owners aren’t happier, don’t sleep better at night.” No opinion on the research itself, but I love the headline.
• Miami has issued a falling iguana warning. (h/t The Prepared)
• “Intimidation is the father of silence and the mother of lies.”
• This building exists.
• Which emoji scissors close?? “If you could file those parts down, you could close [these scissors] a lot more. But you couldn’t, because 📁 is the only file you can get in emoji”. (h/t The Prepared)

Peter Godfrey-Smith’s Other Minds, which is mostly a combination of a discussion on the evolution of intelligence/consciousness and a collection of fun cephalopod anecdotes, surprised me by having a very nice presentation of the core ideas of non-adaptive theories of ageing.

On mutation accumulation:

If we are thinking in evolutionary terms, it’s natural to wonder if there is some hidden benefit from aging itself. Because the onset of aging in our lives can seem so “programmed,” this is a tempting idea. Perhaps old individuals die off because this benefits the species as a whole, by saving resources for the young and vigorous? But this idea is question-begging as an explanation of aging; it assumes that the young are more vigorous. So far in the story, there’s no reason why they should be.

In addition, a situation of this kind is not likely to be stable. Suppose we had a population in which the old do graciously “pass the baton” at some appropriate time, but an individual appeared who did not sacrifice himself in this way, and just kept going. This one seems likely to have the chance to have a few extra offspring. If his refusal to sacrifice was also passed on in reproduction, it would spread, and the practice of sacrifice would be undermined. So even if aging did benefit the species as a whole, that would not be enough to keep it around. This argument is not the end of the line for a “hidden benefit” view, but the modern evolutionary theory of aging takes a different approach. […]

Start with an imaginary case. Assume there is a species of animal with no natural decay over time. These animals show no “senescence,” to use the word preferred by biologists. The animals start reproducing early in their life, and reproduction continues until the animal dies from some external cause—being eaten, famine, lightning strike. The risk of death from these events is assumed to be constant. In any given year, there is a (say) 5 percent chance of dying. This rate does not increase or decrease as you get older, but there is some number of years by which time some accident or other has almost certainly caught you. A newborn has less than a 1 percent chance of still being around at ninety years in this scenario, for example. But if that individual does make it to ninety, it will very probably make it to age ninety-one.

Next we need to look at biological mutations. […] Mutations often tend to affect particular stages in life. Some act earlier, others act later. Suppose a harmful mutation arises in our imaginary population which affects its carriers only when they have been around for many years. The individuals carrying this mutation do fine, for a while. They reproduce and pass it on. Most of the individuals carrying the mutation are never affected by it, because some other cause of death gets them before the mutation has any effect. Only someone who lives for an unusually long time will encounter its bad effects.

Because we are assuming that individuals can reproduce through all their long lives, there is some tendency for natural selection to act against this late-acting mutation. Among individuals who live for a very long time, those without the mutation are likely to have more offspring than those who have it. But hardly anyone lives long enough for this fact to make a difference. So the “selection pressure” against a late-acting harmful mutation is very slight. When molecular accidents put mutations into the population, as described above, the late-acting mutations will be cleaned out less efficiently than early-acting ones.

As a result, the gene pool of the population will come to contain a lot of mutations that have harmful effects on long-lived individuals. These mutations will each become more common, or be lost, mostly through sheer chance, and that makes it likely that some will become common. Everyone will carry some of these mutations. Then if some lucky individual evades its predators and other natural dangers and lives for an unusually long time, it will eventually find things starting to go wrong in its body, as the effects of these mutations kick in. It will appear to have been “programmed to decline,” because the effects of those lurking mutations will appear on a schedule. The population has begun to evolve aging.

On antagonistic pleiotropy:

Is it worth saving enough money so that you will live in luxury when you are 120? Perhaps it is, if you have unlimited money coming in. Maybe you will live that long. But if you don’t have unlimited money coming in, then all the money you save for a long retirement is money you can’t do something else with now. Rather than saving the extra amount needed, it might make more sense to spend it, given that you are not likely to make it to 120 anyway.

The same principle applies to mutations. A lot of mutations have more than one effect, and in some cases, a mutation might have one effect that is visible early in life and another effect that is visible later. If both effects are bad, it is easy to see what will happen—the mutation should be weeded out because of the bad effect it has early in life. It is also easy to see what will happen if both effects are good. But what if a mutation has a good effect now and a bad effect later? If “later” is far enough away that you will probably not make it to that stage anyway, due to ordinary day-to-day risks, then the bad effect is unimportant. What matters is the good effect now. So mutations with good effects early in life and bad effects late in life will accumulate; natural selection will favor them. Once many of these have arisen in the population, and all or nearly all individuals carry some of them, a decay late in life will come to seem preprogrammed. Decay will appear in each individual as if on a schedule, though each individual will show the effects a bit differently. This happens not because of some hidden evolutionary benefit of the breakdown itself, but because the breakdown is the cost paid for earlier gains.

[Mutation accumulation and antagonistic pleiotropy] work together. Once each process gets started, it reinforces itself and also magnifies the other. There is “positive feedback,” leading to more and more senescence. Once some mutations get established that lead to age-related decay, they make it even less likely that individuals will live past the age at which those mutations act. This means there is even less selection against mutations which have bad effects only at that advanced age. Once the wheel starts turning, it turns more and more quickly.

The book discusses various wrinkles in the theory as it applies to different kinds of organisms, then goes on to discuss the question of why most cephalopods are so short-lived. Recommended.

Also posted on the EA Forum; see there for further critique and discussion.

The Weapon of Openness is an essay published by Arthur Kantrowitz and the Foresight Institute in 1989. In it, Kantrowitz argues that the long-term costs of secrecy in adversarial technology development outweigh the benefits, and that openness (defined as “public access to the information needed for the making of public decisions”) will therefore lead to better technology relative to adversaries and hence greater national security. As a result, more open societies will tend to outperform more secretive societies, and policymakers should tend strongly towards openness even in cases where secrecy is tempting in the short-term.

The Weapon of Openness presents itself as a narrow attack on secrecy in technological development. In the process, however, it makes many arguments which seem to generalise to other domains of societal decision-making, and can hence be viewed as a more general attack on certain kinds of secretiveness¹. As such, it seems worth reviewing and reflecting on the arguments in the essay and how they might be integrated with a broader concern for information hazards and the long-term future.

The essay itself is fairly short and worth reading in its entirety, so I’ve tried to keep this fairly brief. Any unattributed blockquotes in the footnotes are from the original text.

Secrecy in technological development

The benefits of secrecy in adversarial technological development are obvious, at least in theory. Barring leaks, infiltration, or outright capture in war, the details of your technology remain opaque to outsiders. With these details obscured, it is much more difficult for adversaries to either copy your technology or design countermeasures against it. If you do really well at secrecy, even the relative power level of your technology remains obscured, which can be useful for game-theoretic reasons².

The costs of secrecy are more subtle, and easier to miss, but potentially even greater than the benefits. This should sound alarm bells for anyone familiar with the failure modes of naïve consequentialist reasoning.

One major cost is cutting yourself off from the broader scientific and technological discourse, greatly restricting the ability of experts outside the project to either propose new suggestions or point out flaws in your current approach. This is bad enough by itself, but it also makes it much more difficult for project insiders to enlist outside expertise during internal disputes over the direction of the project. The result, says Kantrowitz, is that disputes within secret projects have a much greater tendency to be resolved politically, rather than on the technical merits. That means making decisions that flatter the decision-makers, those they favour and those they want to impress, and avoiding changes of approach that might embarrass those people. This might suffice for relatively simple projects that involve making only incremental improvements on existing technology, but when the project aims for an ambitious leap in capabilities (and hence is likely to involve several false starts and course corrections) it can be crippling³.

This claimed tendency of secret projects to make technical decisions on political grounds hints at Kantrowitz’s second major argument⁵: that secrecy greatly facilitates corruption. By screening not only the decisions but the decision-making progress from outside scrutiny, secrecy greatly reduces the incentive for decision-makers to make decisions that could be justified to outside scrutinisers. Given the well-known general tendency of humans to respond to selfish incentives, the result is unsurprising: greatly increased toleration of waste, delay and other inefficiencies, up to and including outright corruption in the narrow sense, when these inefficiencies make the lives of decision-makers or those they favour easier, or increase their status (e.g. by increasing their budget)⁴.

This incentive to corruption is progressive and corrosive, gradually but severely impairing general organisational effectiveness in ways that will obviously impair the effectiveness of the secret project. If the same organisation performs other secret projects in the future, the corrosion will be passed to these successor projects in the form of normalised deviance and generalised institutional decay. Since the corrupted institutions are the very ones responsible for identifying this corruption, and are screened from most or all external accountability, this problem can be very difficult to reverse.

Hence, says Kantrowitz, states that succumb to the temptations of secret technological development may reap some initial gains, but will gradually see these gains eaten away by impaired scientific/technological exchange and accumulating corruption until they are on net far less effective than if they’d stayed open the whole time. The implication of this seems to be that the US and its allies should be tend much more towards openness and less towards secrecy, at least in the technological domain in peacetime⁶.

Secrecy as a short-term weapon

Finally, Kantrowitz makes the interesting argument that secrecy can be a highly effective short-term weapon, even if it isn’t a viable long-term strategy.

When a normally-open society rapidly increases secrecy as a result of some emergency pressure (typically war) they initially retain the strong epistemic institutions and norms fostered by a culture of openness, and can thus continue to function effectively while reaping the adversarial advantages provided by secrecy. In addition, the pressures of the emergency can provide an initial incentive for good behaviour: “the behavior norms of the group recruited may not tolerate the abuse of secrecy for personal advancement or interagency rivalry.”

As such, groups that previously functioned well in the open can continue to function well (or even better) in secret, at least for some short time. If the emergency persists for a long time, however, or if the secret institutions persist past the emergency that created them, the corroding effects of secrecy – on efficacy and corruption – will begin to take root and grow, eventually and increasingly compromising the functionality of the organisation.

Secrecy may therefore be good tactics, but bad strategy. If true, this would explain how some organisations (most notably the Manhatten Project) produce such impressive achievements while remaining highly secretive, while also explaining why these are exceptions to the general rule.

Speculating about this myself, this seems like an ominous possibility: the gains from secrecy are clearly legible and acquired rapidly, while the costs accrue gradually and in a way difficult for an internal actor to spot. The initial successes justify the continuation of secrecy past the period where it provided the biggest gains, after which the accruing costs of declining institutional health make it increasingly difficult to undo. Those initial successes, if later made public, also serve to provide the organisation with a good reputation and public support, while the organisations declining performance in current events are kept secret. As a result, the organisation’s secrecy could retain both public and private support well past the time at which it begins to be a net impediment to efficacy⁷.

If this argument is true, it suggests that secrecy should be kept as a rare, short-term weapon in the policy toolbox. Rather than an indispensible tool of state policy, secrecy might then be regarded analogously to a powerful but addictive stimulant: to be used sparingly in emergencies and otherwise avoided as much as possible.

Final thoughts

The Weapon of Openness presents an important-seeming point in a convincing-seeming way. Its arguments jibe with my general understanding of human nature, incentives, and economics. If true, they seem to present an important counterpoint to concerns about info hazards and information security. At the same time, the piece is an essay, not a paper, and goes to relatively little effort to make itself convincing beyond laying out its central vision: Kantrowitz provides few concrete examples and cites even fewer sources. I am, in general, highly suspicious of compelling-seeming arguments presented without evidentiary accompaniment, and I think I should be even more so when those arguments are in support of my own (pro-academic, pro-openness) leanings. So I remain somewhat uncertain as to whether the key thesis of the article is true.

(One point against that thesis that immediately comes to mind is that a great deal of successful technological development in an open society is in fact conducted in secret. Monetised open-source software aside, private companies don’t seem to be in the habit of publicly sharing their product before or during product development. A fuller account of the weapon of openness would need to account for why private companies don’t fail in the way secret government projects are alleged to⁸.)

If the arguments given in the Weapon of Openness are true, how should those of us primarily concerned with value of the long-term future respond? Long-termists are often sceptical of the value of generalised scientific and technological progress, and in favour of slower, more judicious, differential technological development. The Weapon of Openness suggests this may be a much more difficult needle to thread than it initially seems. We may be sanguine about the slower pace of technological development⁹, but the corrosive effects of secrecy on norms and institutions would seem to bode poorly for the long-term preservation of good values required for the future to go well.

Insofar as this corrosion is inevitable, we may simply need to accept serious information hazards as part of our narrow path towards a flourishing future, mitigating them as best we can without resorting to secrecy. Insofar as it is not, exploring new ways¹⁰ to be secretive about certain things while preserving good institutions and norms might be a very important part of getting us to a good future.

Also posted on the EA Forum.

[Epistemic status: Quick discussion of a seemingly useful concept from a field I as yet know little about.]

I’ve recently started reading around the biosecurity literature, and one concept that seems to come up fairly frequently is the Web of Prevention (also variously called the Web of Deterrence, the Web of Protection, the Web of Reassurance…¹). Basically, this is the idea that the distributed, ever-changing, and dual-use nature of potential biosecurity threats means that we can’t rely on any single strategy (e.g. traditional arms control) to prevent them. Instead, we must rely on a network of different approaches, each somewhat failure-prone, that together can provide robust protection.

For example, the original formulation of the “web of deterrence” identified the key elements of such a web as

comprehensive, verifiable and global chemical and biological arms control; broad export monitoring and controls; effective defensive and protective measures; and a range of determined and effective national and international responses to the acquisition and/or use of chemical and biological weapons².

This later got expanded into a broader “web of protection” concept that included laboratory biosafety and biosecurity; biosecurity education and codes of conduct; and oversight of the life sciences. I’d probably break up the space of strategies somewhat differently, but I think the basic idea is clear enough.

The key concept here is that, though each component of the Web is a serious part of your security strategy, you don’t expect any one to be fully protective or rely on it too heavily. Rather than a simple radial web, a better metaphor might be a multilayered meshwork of protective layers, each of which catches some potential threats while inevitably letting some slip through. No layer is perfect, but enough layers stacked on top of one another can together prove highly effective at blocking attacks³.

This makes sense. Short of a totally repressive surveillance state, it seems infeasible to eliminate all dangerous technologies, all bad actors, or all opportunities to do harm. But if we make means, motive and opportunity each rare enough, we can prevent their confluence and so prevent catastrophe.

Such is the Web of Prevention. In some ways it’s a very obvious idea: don’t put all your eggs in one basket, don’t get tunnel vision, cover all the biosecurity bases. But there’s a few reasons I think it’s a useful concept to have explicitly in mind.

Firstly, I think the concept of the Web of Prevention is important because multilayer protective strategies like this are often quite illegible. One can easily focus too much on one strand of the web / one layer of the armour, and conclude that it’s far too weak to achieve effective protection. But if that layer is part of a system of layers, each of which catches some decent proportion of potential threats, we may be safer than we’d realise if we only focused on one layer at a time.

Secondly, this idea helps explain why so much important biosecurity work consists of dull, incremental improvements. Moderately improving biosafety or biosecurity at an important institution, or tweaking your biocontainment unit protocols to better handle an emergency, or changing policy to make it easier to test out new therapies during an outbreak…none of these is likely to single-handedly make the difference between safety and catastrophe, but each can contribute to strengthening one layer of the system.

Thirdly, and more speculatively, the presence of a web of interlocking protective strategies might mean we don’t always have to make each layer of protection maximally strong to keep ourselves safe. If you go overboard on surveillance of the life sciences, you’ll alienate researchers and shut down a lot of highly valuable research. If you insist on BSL-4 conditions for any infectious pathogens, you’ll burn a huge amount of resources (and goodwill, and researcher time) for not all that much benefit. And so on. Better to set the strength of each layer at a judicious level⁴, and rely on the interlocking web of other measures to make up for any shortfall.

Of course, none of this is to say that we’re actually well-prepared and can stop worrying. Not all strands of the web are equally important, and some may have obvious catastrophic flaws. And a web of prevention optimised for preventing traditional bioattacks may not be well-suited to coping with the biosecurity dangers posed by emerging technologies. Perhaps most importantly, a long-termist outlook may substantially change the Web’s ideal composition and strength. But in the end, I do think I expect something like the Web, and not a single ironclad mechanism, to be what protects us.

Follows from: Why We Age, Part 1; Evolution is Sampling Error; An addendum on effective population size

Last time, I introduced three puzzles in the evolution of ageing:

This, then, is the threefold puzzle of ageing. Why should a process that appears to be so deleterious to the individuals experiencing it have evolved to be so widespread in nature? Given this ubiquity, which implies there is some compelling evolutionary reason for ageing to exist, why do different animals vary so much in their lifespans? And how, when ageing has either evolved or been retained in so many different lineages, have some animals evolved to escape it?

I divided existing theories of the evolution of ageing into two groups, adaptive and nonadaptive, and discussed why one commonly believed nonadaptive theory – namely, simple wear and tear – could not adequately answer these questions.

In this post I’ll discuss other, more sophisticated non-adaptive theories. These theories are characterised by their assertion that ageing provides no fitness benefit to organisms, but rather evolves despite being deleterious to reproductive success. Despite the apparent paradoxicality of this notion, these theories are probably the most widely-believed family of explanations for the evolution of ageing among academics in the field; they’re also the group of theories I personally put the most credence in at present.

How can this be? How can something non-adaptive – even deleterious – have evolved and persisted in so many species across the animal kingdom? To answer this question, we need to understand a few important concepts from evolutionary biology, including genetic drift, relaxed purifying selection, and pleiotropy. First, though, we need to clarify some important terminology.

Mortality, survivorship, and fecundity

For the purposes of this post, a cohort is a group of individuals from the same population who were all born at the same time, i.e. they are of the same age. The survivorship of a cohort at a given age is the percentage of individuals surviving to that age, or equivalently the probability of any given individual surviving at least that long. Conversely, the mortality of a cohort at a given age is the probability of an individual from that cohort dying at that age, and not before or after.

Survivorship and mortality are therefore related, but distinct: survivorship is the result of accumulating mortality at all ages from birth to the age of interest¹. As a result, the mortality and survivorship curves of a cohort will almost always look very different; in particular, while mortality can increase, decrease or stay the same as age increases, survivorship must always decrease. As one important example, constant mortality will give rise to an exponential decline in survivorship².

Four hypothetical mortality curves and their corresponding survivorship curves.

In evolutionary terms, survival is only important insofar as it leads to reproduction. The age-specific fecundity of a cohort is the average number of offspring produced by an individual of that cohort at that age. Crucially, though, you need to survive to reproduce, so the actual number of offspring you are expected to produce at a given age needs to be downweighted in proportion to your probability of dying beforehand. This survival-weighted fecundity (let’s call it your age-specific reproductive output) can be found by multiplying the age-specific fecundity by the corresponding age-specific survivorship. Since this depends on survivorship, not mortality, it will tend to decline with age: a population with constant mortality and constant fecundity (i.e. no demographic ageing) will show reproductive output that declines exponentially along with survivorship.

Two hypothetical mortality/fecundity curves and their corresponding reproductive outputs.

The fitness of an individual is determined by their lifetime reproductive output (i.e. the total number of offspring they produce over their entire lifespan)⁴. Mutations that significantly decrease lifetime reproductive output will therefore be strongly opposed by natural selection. It seems mutations leading to ageing (i.e. an increase in mortality and decrease in fecundity with time) should be in that category. So why does ageing evolve?

What good is immortality?

Imagine a race of beautiful, immortal, ageless beings — let’s call them elves. Unlike we frail humans, elves don’t age: they exhibit constant mortality and constant fecundity. As a result, their age-specific survivorship and reproductive output both fall off exponentially with increasing age — far more slowly, in other words, than occurs in humans.

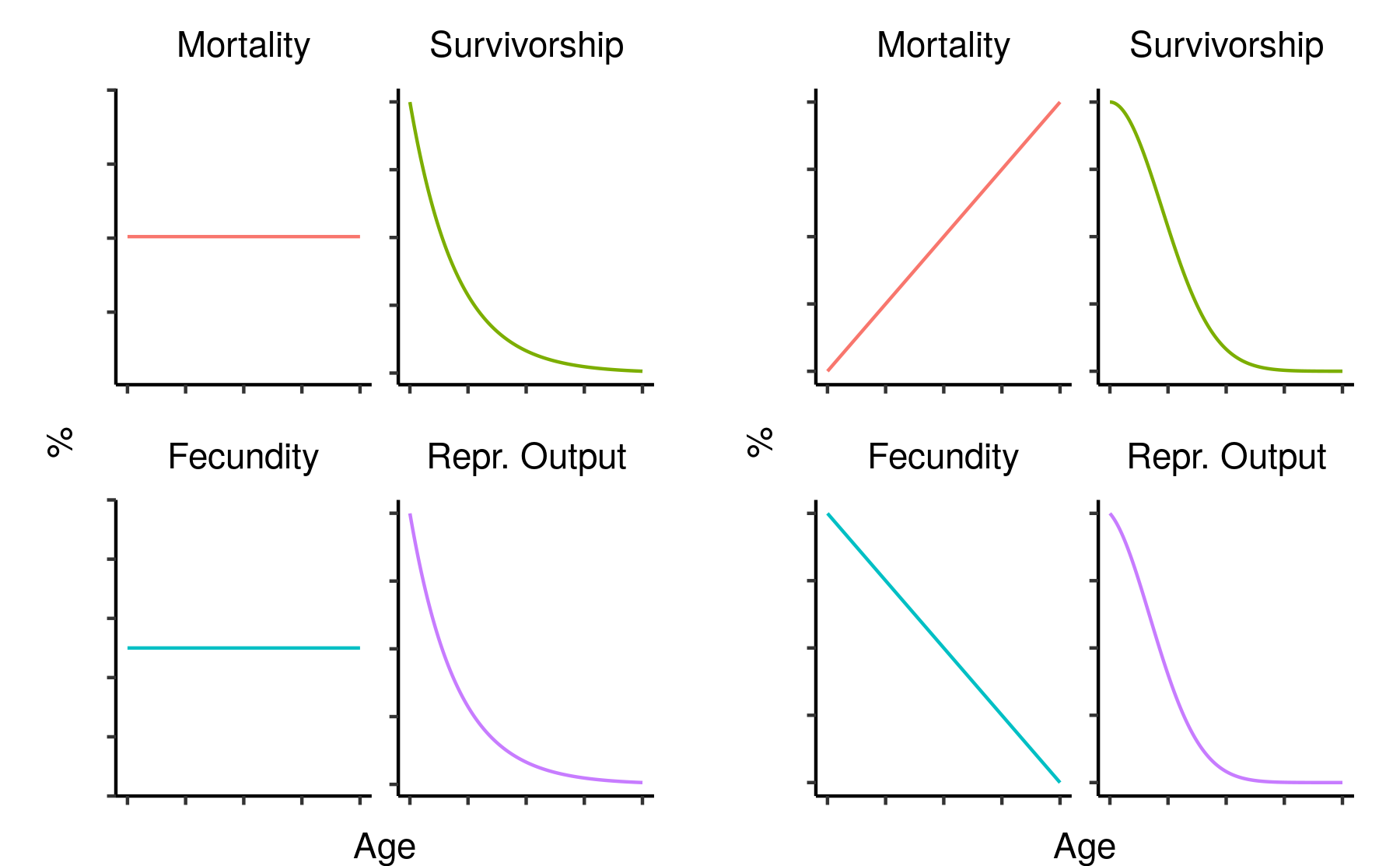
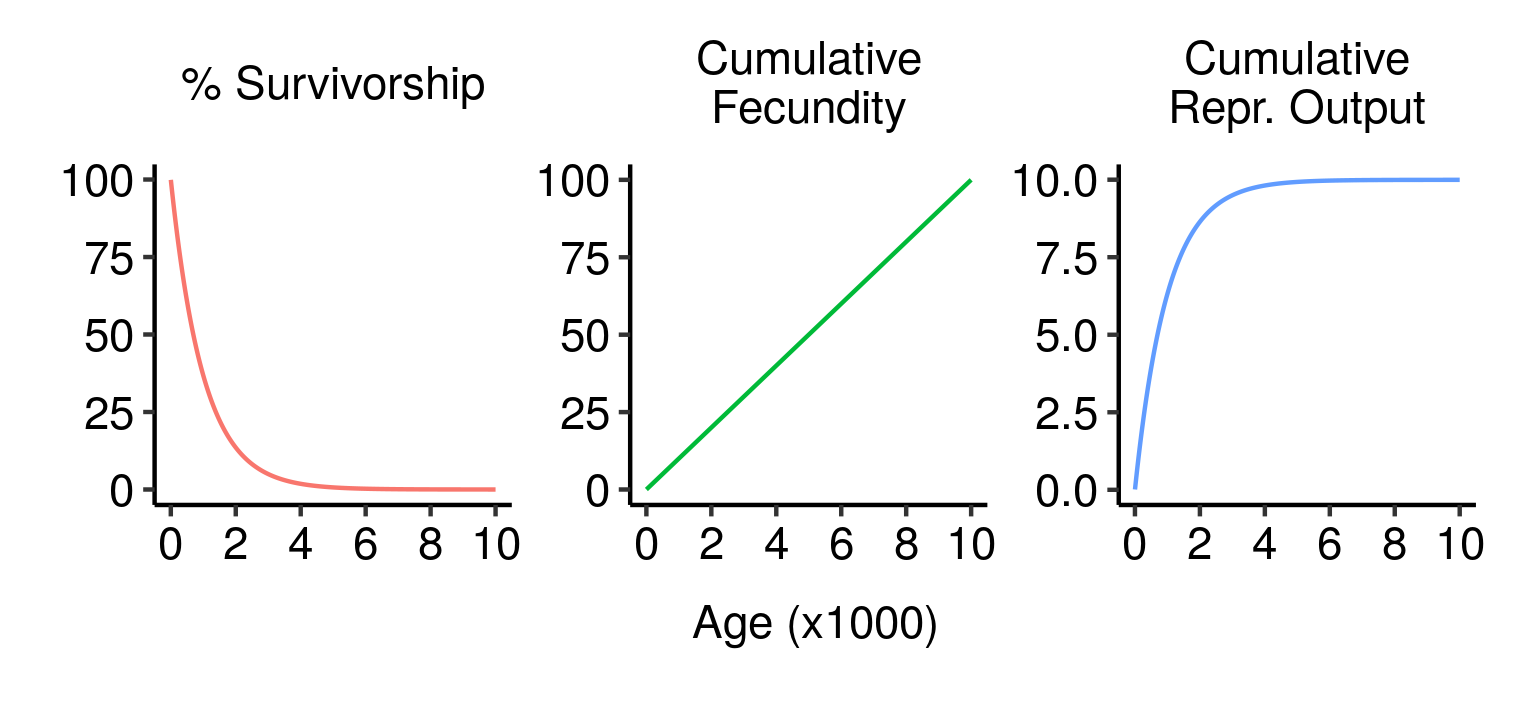Survivorship, cumulative fecundity and cumulative reproductive output curves for a population of elves with 1% fecundity and 0.1% mortality per year.

Under the parameters I’ve used here (1% fecundity, 0.1% mortality), an elf has about a 50% chance of making it to 700 years old and a 10% chance of living to the spry old age of 2,300. An elf that makes it that far will have an average of 23 children over its life; 7 if it only makes it to the median lifespan of 700.

Since fecundity and mortality are constant, an elf that makes it to 3,000 will be just as fit and healthy then as they were as a mere stripling of 500, and will most likely still have a long and bright future ahead of them. Nevertheless, the chance of any given newborn elf making it that far is small (about 5%). This means that, even though an old elf could in principle have as many children as a much younger individual elf, the actual offspring in the population are mainly produced by younger individuals. Just over 50% of the lifetime expected reproductive output of a newborn elf is concentrated into its first 700 years; even though it could in principle live for millennia, producing children at the same rate all the while, its odds of reproducing are best early in life. You can, after all, only breed when you’re living.

This fact — that reproductive output is concentrated in early life even in the absence of ageing — has one very important consequence: natural selection cares much more about you when you’re young.

Natural selection is ageist

No genome is totally stable — mutations always occur. Let’s imagine that three mutations arise in our elven population. Each is fatal to its bearer, but with a time delay, analogous to Huntington’s disease or some other congenital diseases in humans. Each mutation has a different delay, taking effect respectively at 100, 1000, and 10000 years of age. What effect will these mutations have on their bearers’ fitness, and how well will they spread in the population?

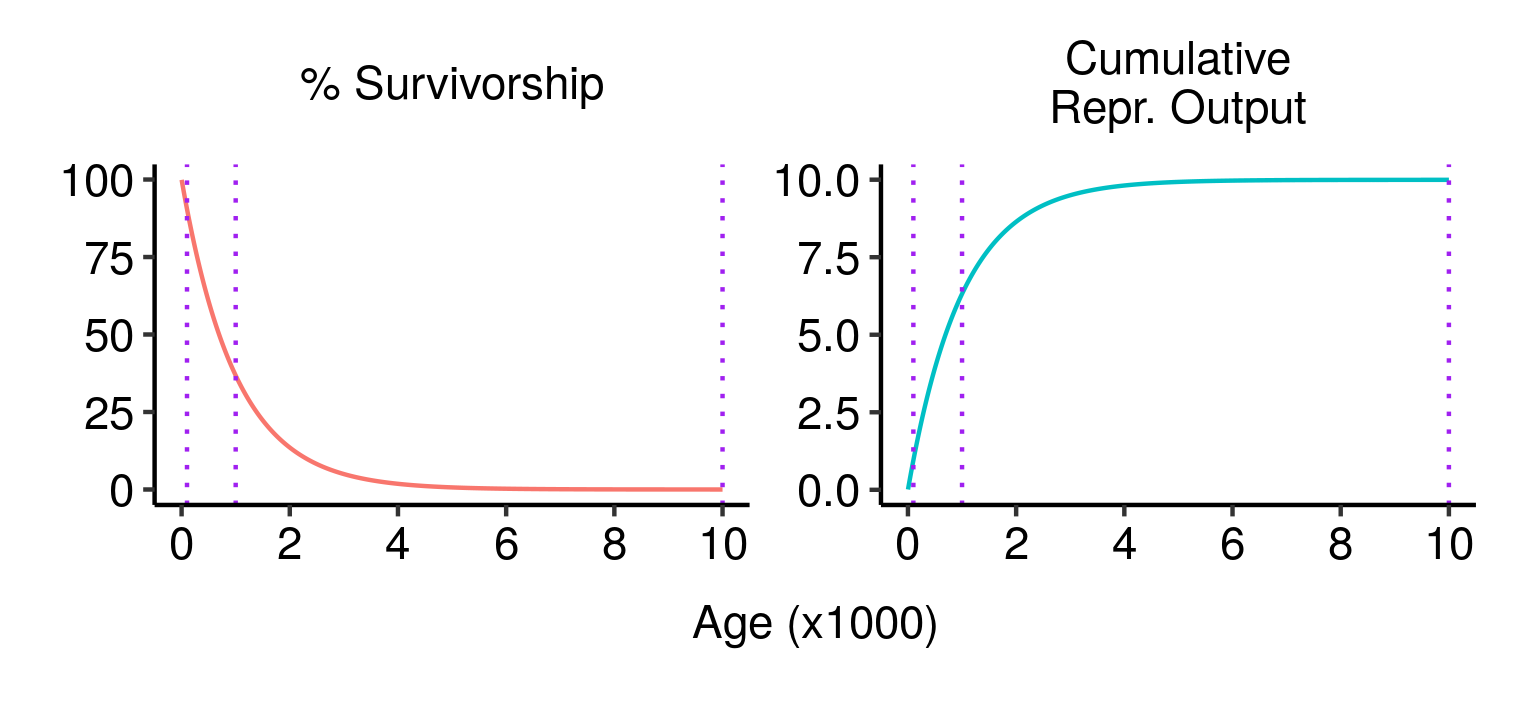Three potential fatal mutations in the elven populations, and their effects on lifetime reproductive output.

Although all three mutations have similar impacts on an individual who lives long enough to experience them, from a fitness perspective they are very different. The first mutation is disastrous: almost 90% of wild-type individuals (those without the mutation) live past age 100, and a guaranteed death at that age would eliminate almost 90% of your expected lifetime reproductive output. The second mutation is still pretty bad, but less so: a bit over a third of wild-type individuals live to age 1000, and dying at that age would eliminate a similar proportion of your expected lifetime reproductive output. The third mutation, by contrast, has almost no expected effect: less than 0.005% of individuals make it to that age, and the effect on expected lifetime reproductive output is close to zero. In terms of fitness, the first mutation would be strenuously opposed by natural selection; the second would be at a significant disadvantage; and the third would be virtually neutral.

This extreme example illustrates a general principle:

The impact of a mutation on the fitness of an organism depends on both the magnitude of its effect and the proportion of total reproductive output affected.

— Williams 1957 ⁵

Mutations that take effect later in life affect a smaller proportion of total expected reproductive output and so have a smaller selective impact, even if the size of the effect when they do take effect is just as strong. The same principle applies to mutations with less dramatic effects: those that affect early-life survival and reproduction have a big effect on fitness and will be strongly selected for or against, while those that take effect later will have progressively less effect on fitness and will thus be exposed to correspondingly weaker selection pressure. Put in technical language, the selection coefficient of a mutation depends upon the age at which it takes effect, with mutations affecting later life having coefficients closer to zero.

Evolution is sampling error, and selection is sampling bias. When the selection coefficient is close to zero, this bias is weak, and the mutation’s behaviour isn’t much different from that of a neutral mutation. As such, mutations principally affecting later-life fitness will act more like neutral mutations, and increase and decrease in frequency in the population with little regard for their effects on those individuals that do live long enough to experience them. As a result, while mutations affecting early life will be purged from the population by selection, those affecting late life will be allowed to accumulate through genetic drift. Since the great majority of mutations are negative, this will result in deteriorating functionality at older ages.

So our elves are sadly doomed to lose their immortality, unless something very weird is happening to cause them to keep it. Mutations impairing survival and reproduction early in life will be strenuously removed by natural selection, but those causing impairments later in life will accumulate, leading to a progressive increase in mortality and decline in fecundity. This might seem bad enough, but unfortunately there is more bad news on the horizon — because this isn’t the only way that nonadaptive ageing can evolve.

Perverse trade-offs

Imagine now that instead of a purely negative, Huntingdon-like mutation arising in our ageless elf population, a mutation arose that provided some fitness benefit early in life at the cost of some impairment later; perhaps promoting more investment in rapid growth and less in self-repair, or disposing the bearer more towards risky fights for mates. How would this new mutation behave in the population?

The answer depends on the magnitude of the early-life benefit granted by the mutation, as well as of its later-life cost. However, we already saw that in weighing this trade-off natural selection cares far more about fitness in early life than in later life; as such, even a mutation whose late-life cost far exceeded its early-life benefit in magnitude could be good for overall lifetime fitness, and hence have an increased chance of spreading and becoming fixed in the population. Over time, the accumulation of mutations like this could lead to ever-more-severe ageing in the population, even as the overall fitness of individuals in the population continues to increase.

This second scenario, in which the same mutation provides a benefit at one point in life and a cost at another, is known as antagonistic pleiotropy⁶. It differs from the mutation accumulation theory of ageing outlined above in that, while in the former case ageing arises primarily through genetic drift acting on late-life-affecting deleterious mutations, the latter proposes that ageing arises as a non-adaptive side effect of a fitness-increasing process. Both theories are “non-adaptive” in that the ageing that results is not in itself good for fitness, and both depend on the same basic insight: due to inevitably declining survivorship with age, the fitness effect of a change in survival or reproduction tends to decline as the age at which it takes effect increases.

Mutation accumulation and antagonistic pleiotropy have historically represented the two big camps of ageing theorists, and the theories have traditionally been regarded as being in opposition to each other. I’ve never really understood why, though: the basic insight required to understand both theories is the same, and conditions that gave rise to ageing via mutation accumulation could easily also give rise to additional ageing via antagonistic pleiotropy⁷. Importantly, both theories give the same kinds of answers to the other two key questions of ageing I discussed last time: why do lifespans differ between species, and why do some animals escape ageing altogether?

It’s the mortality, stupid

As explanations of ageing, both mutation accumulation and antagonistic pleiotropy depend on extrinsic mortality; that is, probability of death arising from environmental factors like predation or starvation. As long as extrinsic mortality is nonzero, survivorship will decline monotonically with age, resulting (all else equal) in weaker and weaker selection agains deleterious mutations affecting later ages. The higher the extrinsic mortality, the faster the decline in survivorship with age, and the more rapid the corresponding decline in selection strength.

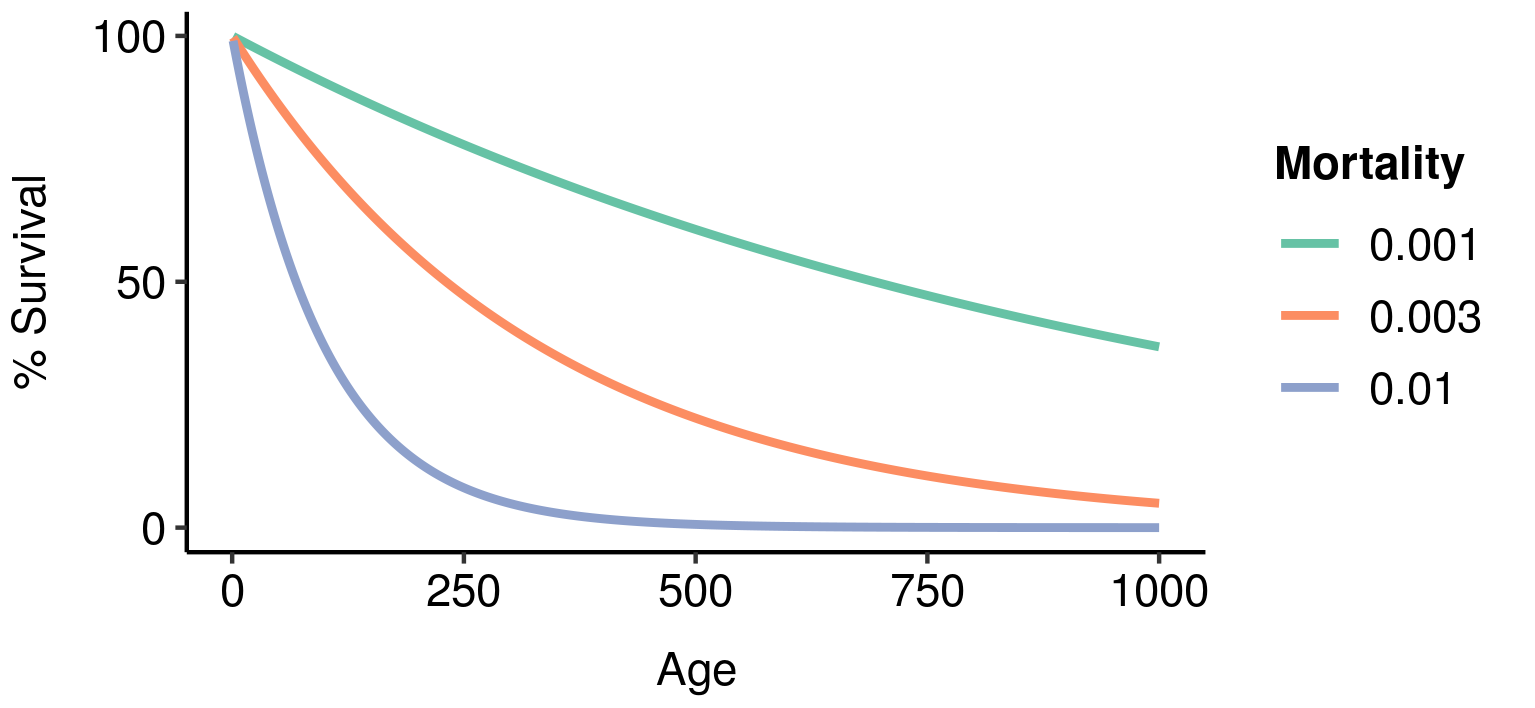Age-specific survivorship as a function of different levels of constant extrinsic mortality.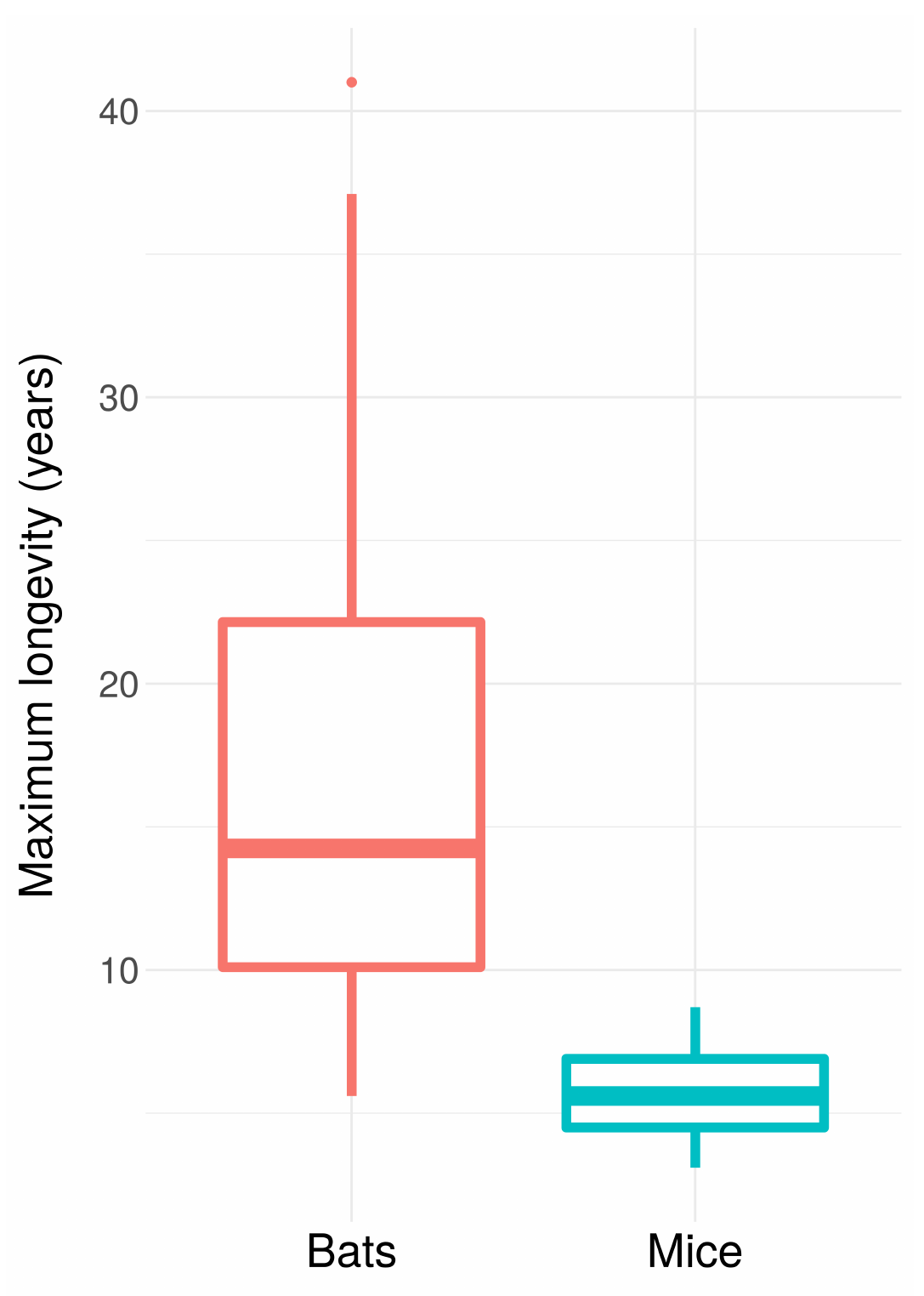

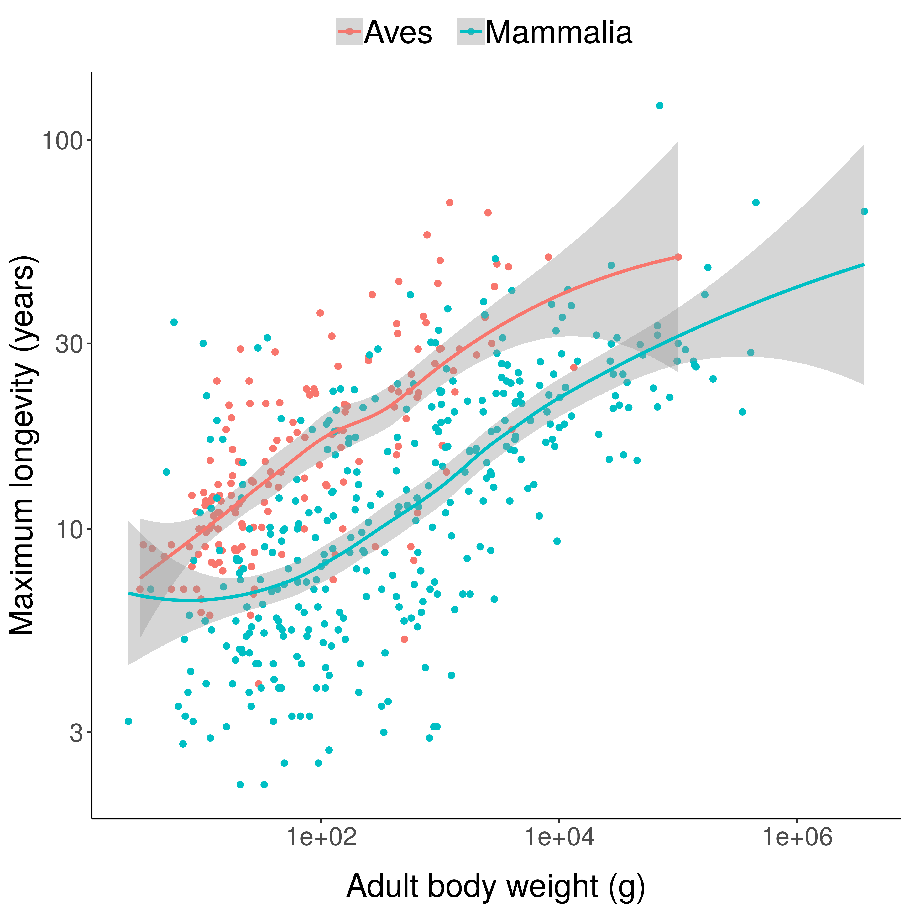As a result, lower extrinsic mortality will generally result in slower ageing: your chance of surviving to a given age is higher, so greater functionality at that age is more valuable, resulting in a stronger selection pressure to maintain that functionality.

This is the basic explanation for why bats live so much longer than mice despite being so similar: they can fly, which protects them from predators, which reduces their extrinsic mortality.

You can see something similar if you compare all birds and all mammals, controlling for body size (being larger also makes it harder to eat you):

Scatterplots of bird and mammal maximum lifespans vs adult body weight from the AnAge database, with central tendencies fit in R using local polynomial regression (LOESS).

In addition to body size and flight, you are also likely to have a longer lifespan if you are⁸:

• Arboreal
• Burrowing
• Poisonous
• Armoured
• Spiky
• Social

All of these factors share the property of making it harder to predate you, reducing extrinsic mortality. In many species, females live longer than males even in captivity: males are more likely to (a) be brightly coloured or otherwise ostentatious, increasing predation, and (b) engage in fights and other risky behaviour that increases the risk of injury. I’d predict that other factors that reduce extrinsic mortality in the wild (e.g. better immune systems, better wound healing) would similarly correlate with longer lifespans in safe captivity.

This, then, is the primary explanation non-adaptive ageing theories give for differences in rates of ageing between species: differences in extrinsic mortality. Mortality can’t explain everything, though: in particular, since mortality is always positive, resulting in strictly decreasing survivorship with increasing age, it can’t explain species that don’t age at all, or even age in reverse (with lower intrinsic mortality at higher ages).

It’s difficult to come up with a general theory for non-ageing species, many of which have quite ideosyncratic biology; one might say that all ageing species are alike, but every non-ageing species is non-ageing in its own way. But one way to get some of the way there is to notice that mortality/survivorship isn’t the only thing affecting age-specific reproductive output; age-specific fecundity also plays a crucial role. If fecundity increases in later ages, this can counterbalance, or even occasionally outweigh, the decline in survivorship and maintain the selective value of later life.

Mammals and birds tend to grow, reach maturity, and stop growing. Conversely, many reptile and fish species keep growing throughout their lives. As you get bigger, you can not only defend yourself better (reducing your extrinsic mortality), but also lay more eggs. As a result, fecundity in these species increases over time, resulting – sometimes – in delayed or even nonexistent ageing:

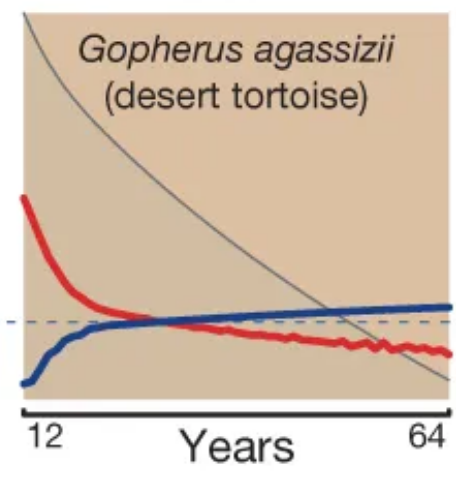Mortality (red) and fertility (blue) curves from the desert tortoise, showing declining mortality with time. Adapted from Fig. 1 of Jones et al. 2014.

So that’s one way a species could achieve minimal/negative senescence under non-adaptive theories of ageing: ramp up your fecundity to counteract the drop in survivorship. Another way would be to be under some independent selection pressure to develop systems (like really good tissue regeneration) that incidentally also counteract the ageing process. Overall, though, it seems to be hard to luck yourself into a situation that avoids the inexorable decline in selective value imposed by falling survivorship, and non-ageing animal species are correspondingly rare.

Next time in this series, we’ll talk about the other major group of theories of ageing: adaptive ageing theories. This post will probably be quite a long time coming since I don’t know anything about adaptive theories right now and will have to actually do some research. So expect a few other posts on different topics before I get around to talking about the more heterodox side of the theoretical biology of ageing.

Happy New Year! More links abound. As always, these are “new” only in the sense that I read them recently; some of them are actually quite old.

• More on the Blackmail Paradox: David Henderson and Robin Hanson in favour of legalising blackmail, Tyler Cowen, Scott Sumner and Paul Christiano against. Hanson has written a lot on this; see the linked post for extra links if you want to go digging. Currently I feel the theoretical arguments probably support legalising blackmail, but this feels like one of those Secret-Of-Our-Success-y cases where tradition says blackmail should be illegal and we don’t have a compelling enough case to risk screwing around with it.
• Given Aumann’s agreement theorem, should you persist in disagreeing with a painted rock? Should you double-crux with one?
• “However, it is unfortunate that for billions of people worldwide, the quadratic formula is also their first (and perhaps only) experience of a rather complicated formula which they must memorize. Countless mnemonic techniques abound, from stories of negative bees considering whether or not to go to a radical party, to songs set to the tune of Pop Goes the Weasel.”
• I’m pretty confused about flossing and I think you should be too.
• A classic in observer selection effects from Nick Bostrom: cars in the next lane really do go faster.
• Rather than steal a load of cool links from another linkpost, here’s the post itself. I can’t vouch for their epistemic standards though.
• There are at least 4,500 speakers of Kannada in Canada. All of whom are presumably delighted that you’ve brought up how funny that is.
• Wikipedia has a dedicated talk page for arguing about the spelling of alumin(i)um. I don’t have strong feelings about it¹, but it’s undeniably entertaining. See also Wikipedia’s list of lamest edit wars.
• A university in Serbia is accused of plagiarising a research ethics code from another university. On the one hand, this is obviously pretty funny, but on the other if I’d produced a research ethics code I thought was good I think I’d want as many people as possible to copy it, with or without credit.
• I’ve seen some bad websites in my time, but this one achieves the dubious feat of being genuinely physically painful to read. I’m not sure why I’m sharing this.
• British naming habits have changed a lot in the last 30 years.
• Andrew Gelman points out that the opposite of “black box” is not, in fact, white box.
• I always vaguely assumed that “never send to know for whom the bell tolls; it tolls for thee” was some sort of memento mori thing, but it turns out I was totally wrong about this, as reading the whole poem makes clear. I might memorise this one. I also never realised before that “for whom the bell tolls” and “no man is an island” are quotes from the same poem, so TIL.

Follows from: Evolution is Sampling Error

It seems a lot of people either missed my footnotes in the last post about effective population size, or noticed them, read them and were confused¹. I think the second response is reasonable; for non-experts, the concept of effective population size is legitimately fairly confusing. So I thought I’d follow up with a quick addendum about what effective population size is and why we use it. Since I’m not a population geneticist by training this should also be a useful reminder for me.

The field of biology that deals with the evolutionary dynamics of populations — how mutations arise and spread, how allele frequencies shift over time through drift and selection, how alleles flow between partially-isolated populations — is population genetics. “PopGen” differs from most of biology in that its foundations are primarily hypothetico-deductive rather than empirical: one begins by proposing some simple model of how evolution works in a population, then derives the mathematical consequences of those initial assumptions. A very large and often very beautiful edifice of theory has been constructed from these initial axioms, often yielding surprising and interesting results.

Population geneticists can therefore say a great deal about the evolution of a population, provided it meets some simplifying assumptions. Unfortunately, real populations often violate these assumptions, often dramatically so. When this happens, the population becomes dramatically harder to model productively, and the maths becomes dramatically more complicated and messy. It would therefore be very useful if we could find a way to usefully model more complex real populations using the models developed for the simple cases.

Fortunately, just such a hack exists. Many important ways in which real populations deviate from ideal assumptions cause the population to behave roughly like an idealised population of a different (typically smaller) size. This being the case, we can try to estimate the size of the idealised population that would best approximate the behaviour of the real population, then model the behaviour of that (smaller, idealised) population instead. The size of the idealised population that causes it to best approximate the behaviour of the real population is that real population’s “effective” size.

There are various ways in which deviations from the ideal assumptions of population genetics can cause a population to act as though it were smaller – i.e. to have an effective size (often denoted \(N_e\)) that is smaller than its actual census size – but two of the most important are non-constant population size and, for sexual species, nonrandom mating. According to Gillespie (1998), who I’m using as my introductory source here, fluctuations in population size are often by far the most important factor.

In terms of some of the key equations of population genetics, a population whose size fluctuates between generations will behave like a population whose constant size is the harmonic mean of the fluctuating sizes. Since the harmonic mean is much more sensitive to small values than the arithmetic mean, this means a population that starts large, shrinks to a small size and then grows again will have a much smaller effective size than one that remains large². Transient population bottlenecks can therefore have dramatic effects on the evolutionary behaviour of a population.

Many natural populations fluctuate wildly in size over time, both cyclically and as a result of one-off events, leading to effective population sizes much smaller than would be expected if population size were reasonably constant. In particular, the human population as a whole has been through multiple bottlenecks in its history, as well as many more local bottlenecks and founder effects occurring in particular human populations, and has recently undergone an extremely rapid surge in population size. It should therefore not be too surprising that the human \(N_e\) is dramatically smaller than the census size; estimates vary pretty widely, but as I said in the footnotes to the last post, tend to be roughly on the order of \(10^4\).

In sexual populations, skewed sex ratios and other forms of nonrandom mating will also tend to reduce the effective size of a population, though less dramatically³; I don’t want to go into too much detail here since I haven’t talked so much about sexual populations yet.

As a result of these and other factors, then, the effective sizes of natural populations is often much smaller than their actual census sizes. Since genetic drift is stronger in populations with smaller effective sizes, that means we should expect populations to be much more “drifty” than you would expect if you just looked at their census sizes. As a result, evolution is typically more dominated by drift, and less by selection, than would be the case for an idealised population of equivalent (census) size.